
힙(Heap)은 컴퓨터 과학에서 널리 사용되는 중요한 데이터 구조 중 하나입니다. 이번 글에서는 힙이 무엇인지, 어떻게 구성되는지, 그리고 어떻게 활용되는지에 대해 알아보겠습니다. 특히, 힙이 Complete Binary Tree(완전 이진 트리)라는 속성을 가지고 있으며, 우선순위 큐(priority queue)를 구현하는 데 사용된다는 점을 강조할 것입니다.
힙 데이터 구조 소개
힙은 완전 이진 트리로 구성됩니다. 여기서 완전 이진 트리란 마지막 레벨을 제외한 모든 레벨이 꽉 차 있고, 마지막 레벨의 노드들이 왼쪽부터 차례대로 채워진 트리를 말합니다. 이러한 특성은 배열을 사용하여 효율적으로 구현할 수 있습니다.
Max Heap과 Min Heap
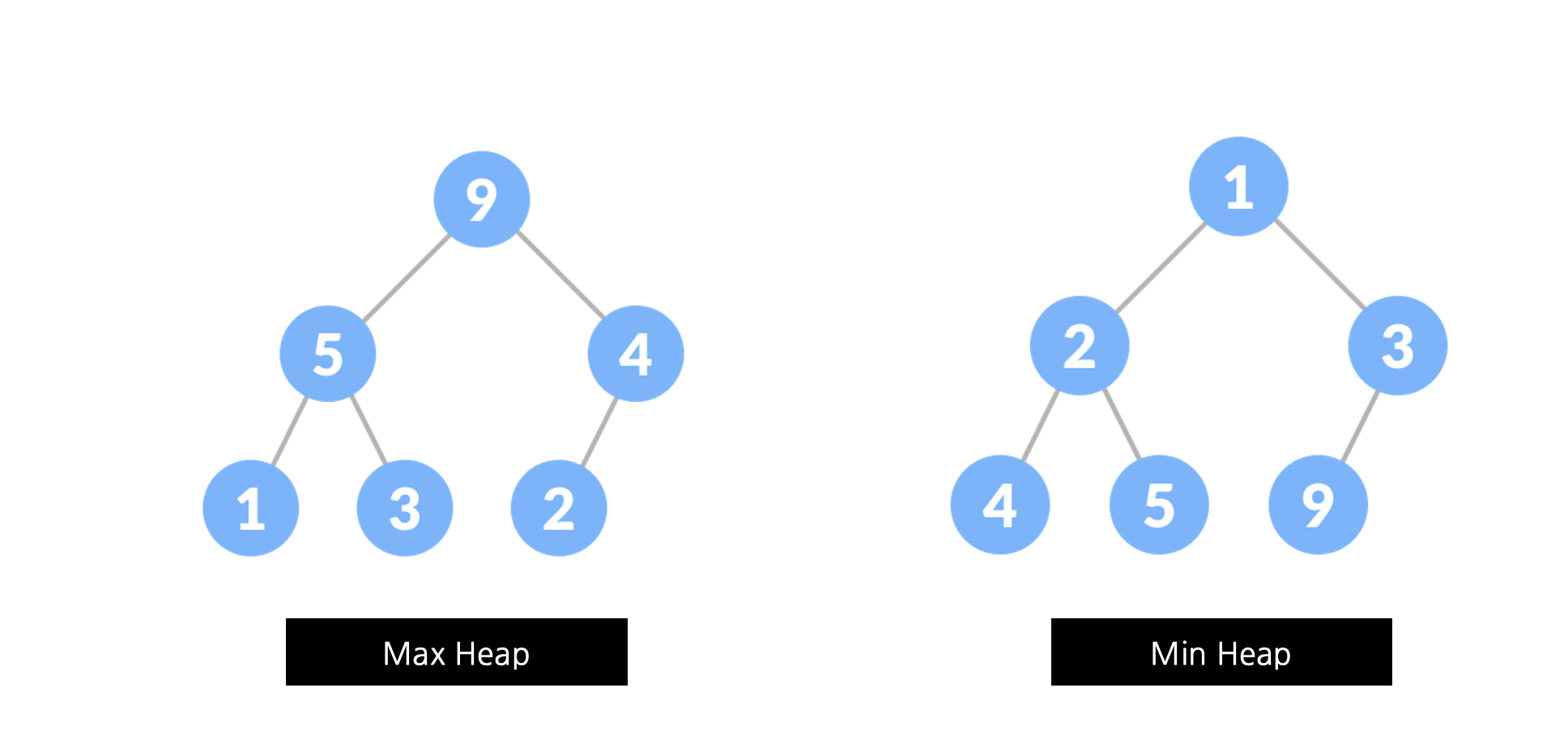
힙은 두 가지 주요 유형으로 나뉩니다: Max Heap과 Min Heap입니다. Max Heap은 루트 노드가 가장 큰 값을 가지고 있고, 모든 부모 노드가 자식 노드보다 크거나 같은 속성을 갖습니다. 이는 우선순위 큐에서 가장 큰 우선순위를 갖는 요소를 찾거나 삭제할 때 유용합니다. 반면 Min Heap은 루트 노드가 가장 작은 값을 가지고 있으며, 부모 노드가 자식 노드보다 작거나 같은 속성을 갖습니다. 이는 최솟값을 찾거나 삭제할 때 유용합니다.
힙 데이터 구조 - Complete Binary
- Max Heap : 상위노드가 항상 하위 노드보다 크고 루트 노드의 키는 다른 모든 노드 중에서 가장 큽니다. 이 속성은 최대 힙 속성- Min Heap : 상위노드가 항상 하위 노드보다 작으며 루트 노드의 키는 다른 모든 노드 중에서 가장 작습니다. 이 속성은 최소 힙 속성Heap의 조건 (Complete Binary Tree)
- 마지막 레벨을 제외한 각 레벨엔 빠짐없이 노드가 존재
- 마지막 레벨의 노드는 왼쪽부터 차례대로 빈틈없이 채워짐
힙의 활용
힙은 우선순위 큐를 구현하는 데 주로 사용됩니다. 우선순위 큐는 가장 높은 우선순위를 가진 요소를 먼저 제거하는 자료구조입니다. 힙을 사용하면 우선순위 큐의 삽입, 삭제, 최댓값 또는 최솟값 검색 등의 작업을 효율적으로 수행할 수 있습니다.
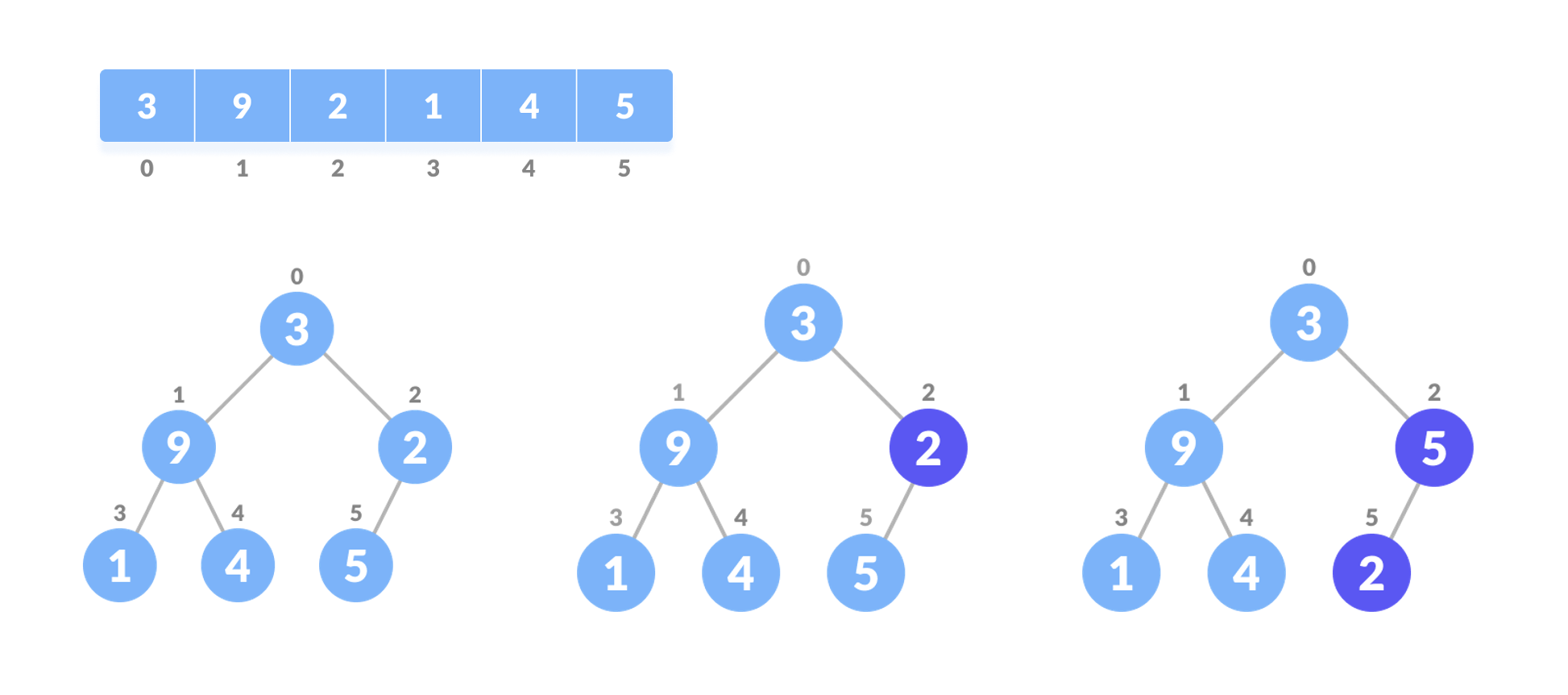
1. A[k]의 자식노드는 A[2k+1], A[2k+2]ex 2.) A[k]의 부모노드는 A[(k-1)/2]를 통해 접근 가능
2. 첫번째 비단말 노드 확인 : 주어진 배열은 [3, 9, 2, 1, 4, 5] 입니다.
3. 배열에서 n/2 - 1 인덱스를 가진 첫 번째 비단말 노드를 확인 여기서 n은 배열의 크기, 즉 6이므로, n/2 - 1은 2가 됨.
따라서, 인덱스 2에 위치한 값 2가 첫 번째 비단말 노드가 됨.
4. 인덱스 2(값 2)를 현재 요소로 설정하고, 왼쪽 자식의 인덱스는 2*2 + 1 = 5가 되므로 값은 5입니다.
5. 오른쪽 자식은 없습니다 (인덱스 범위를 넘어감).왼쪽 자식 5가 현재 요소 2보다 크므로, 왼쪽 자식을 가장 큰 요소로 설정합니다.
6. 가장 큰 요소인 왼쪽 자식 5와 현재 요소 2를 교환합니다.
7. 교환한 결과, 배열은 [3, 9, 5, 1, 4, 2]가 됩니다.인덱스 5에 있는 2에 대해 하위 트리를 힙화할 필요가 없습니다, 왜냐하면 더 이상 자식 노드가 없기 때문입니다.
결론
힙은 컴퓨터 과학에서 중요한 자료구조 중 하나로, Complete Binary Tree의 속성을 갖습니다. 이를 활용하여 우선순위 큐를 구현할 수 있으며, Max Heap과 Min Heap의 특성을 통해 효율적으로 데이터를 관리할 수 있습니다. 힙을 잘 이해하고 활용한다면 다양한 알고리즘 및 데이터 구조 문제를 해결하는 데 도움이 될 것입니다.
우선순위 큐(Priority Queue)는 각 요소가 우선순위 값과 연관되어 있는 특별한 유형의 대기열입니다. 이것은 FIFO(First-In-First-Out) 대기열과는 다르게, 요소들이 우선순위에 따라 처리됩니다. 즉, 높은 우선순위를 갖는 요소가 낮은 우선순위를 갖는 요소보다 먼저 처리됩니다. 이것은 일상생활에서 VIP가 다른 사람들보다 먼저 서비스를 받는 것과 유사합니다.

우선순위 큐를 구현할 때, 이진힙(Heap) 자료구조를 사용하는 것이 일반적입니다. 이진힙은 완전이진트리(Complete Binary Tree)로서, 부모 노드의 값이 자식 노드의 값보다 항상 크거나 작은 성질을 가집니다. 이를 통해 우선순위 큐의 삽입(insert)과 삭제(delete) 연산을 O(logn)의 시간 복잡도로 수행할 수 있습니다.

우선순위 큐를 이진힙으로 구현하는 방법은 다음과 같습니다.

- 삽입(Insert)
새로운 요소를 대기열의 끝에 추가합니다. 이후, 이진힙 성질을 유지하기 위해 Heapify 과정을 수행합니다. Heapify는 새로운 요소를 부모 노드와 비교하여 필요에 따라 위치를 조정하는 과정입니다. - 삭제(Delete): 삭제할 요소를 선택 합니다. 이후, 해당 요소를 마지막 리프 노드와 교체합니다. 그리고 마지막 요소를 리프에서 제거한 후, 이진힙 성질을 다시 유지하기 위해 Heapify 과정을 수행합니다.

이러한 과정을 통해 우선순위 큐를 이진힙으로 구현할 수 있습니다. 코드로 구현한다면 다음과 같을 것입니다.
class PriorityQueue:
def __init__(self):
self.heap = []
def insert(self, element):
self.heap.append(element)
self.heapify_up(len(self.heap) - 1)
def delete(self):
if len(self.heap) == 0:
return None
if len(self.heap) == 1:
return self.heap.pop()
deleted_element = self.heap[0]
self.heap[0] = self.heap.pop()
self.heapify_down(0)
return deleted_element
def heapify_up(self, index):
parent_index = (index - 1) // 2
if index > 0 and self.heap[index] < self.heap[parent_index]:
self.heap[index], self.heap[parent_index] = self.heap[parent_index], self.heap[index]
self.heapify_up(parent_index)
def heapify_down(self, index):
left_child_index = 2 * index + 1
right_child_index = 2 * index + 2
smallest = index
if left_child_index < len(self.heap) and self.heap[left_child_index] < self.heap[smallest]:
smallest = left_child_index
if right_child_index < len(self.heap) and self.heap[right_child_index] < self.heap[smallest]:
smallest = right_child_index
if smallest != index:
self.heap[index], self.heap[smallest] = self.heap[smallest], self.heap[index]
self.heapify_down(smallest)
# 우선순위 큐 사용 예시
pq = PriorityQueue()
pq.insert(5)
pq.insert(3)
pq.insert(7)
pq.insert(1)
print(pq.delete()) # 출력: 1
print(pq.delete()) # 출력: 3
이렇게 구현된 우선순위 큐는 이진힙의 특성을 이용하여 요소들을 삽입하고 삭제할 수 있습니다. 이를 통해 우선순위에 따라 요소들을 효율적으로 처리할 수 있습니다. 따라서 우선순위큐는 이진힙과 비슷하다고 볼 수 있습니다.